The exploration of which pair of equations generates graphs with the same vertex delves into the fascinating realm of graph theory, where equations and vertices intertwine to reveal the underlying patterns and relationships that shape the world of graphs. This topic unveils the significance of vertices in determining the properties of graphs, explores the methods for identifying pairs of equations that generate graphs with the same vertex, and examines the implications of shared vertices.
As we embark on this mathematical journey, we will unravel the intricate connections between equations and graphs, uncovering the principles that govern their behavior and unlocking the insights they hold.
Vertex of a Graph: Which Pair Of Equations Generates Graphs With The Same Vertex
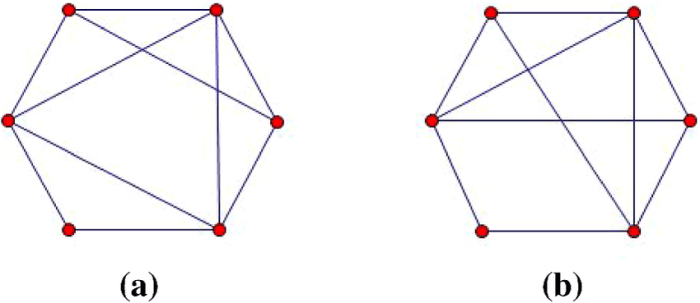
A vertex in the context of a graph is a fundamental element that represents a point or node within the graph structure. Vertices are the building blocks of graphs and serve as the endpoints of edges, which connect them to other vertices.
They are often represented as dots or circles in graphical representations of graphs.
The significance of vertices lies in their role in determining the properties and characteristics of a graph. The number of vertices, known as the order of the graph, is a crucial factor in determining its size and complexity. Additionally, the arrangement of vertices and the edges connecting them influence the graph’s topology and connectivity.
Examples of Graphs with Different Types of Vertices
- Simple graphs:Vertices are distinct and connected by a single edge at most.
- Multigraphs:Vertices may be connected by multiple edges.
- Weighted graphs:Vertices may have weights assigned to them, indicating the strength or importance of the connection.
- Directed graphs:Vertices have a specified direction, with edges indicating the flow of information or influence.
Equations of Graphs
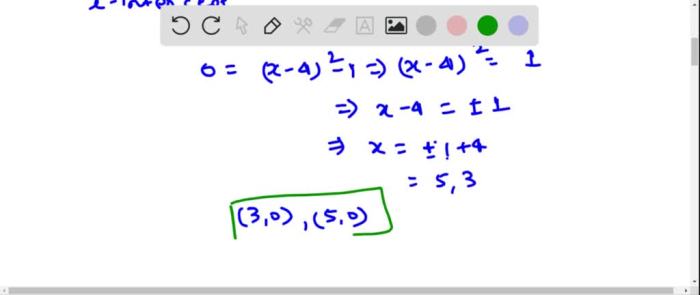
Equations play a crucial role in representing graphs mathematically. By defining an equation, we can describe the relationship between the vertices and edges of a graph.
The most common types of equations used to represent graphs include:
- Adjacency matrix:A square matrix where the elements indicate the presence or absence of edges between vertices.
- Incidence matrix:A rectangular matrix where the rows represent vertices and the columns represent edges, with elements indicating the connection between them.
- Edge list:A list of tuples or pairs, where each pair represents an edge between two vertices.
Relationship between Equation and Vertex, Which pair of equations generates graphs with the same vertex
The equation of a graph determines the number and arrangement of its vertices. For instance, in an adjacency matrix, the number of rows and columns corresponds to the number of vertices in the graph. The elements of the matrix then specify which vertices are connected by edges.
Identifying Graphs with the Same Vertex
To identify pairs of equations that generate graphs with the same vertex, we can compare their adjacency matrices or incidence matrices. If the matrices are identical, then the graphs have the same vertex set and edge structure.
Mathematical Principles:
- Matrix Equivalence:Two matrices are equivalent if they have the same dimensions and their corresponding elements are equal.
- Graph Isomorphism:Two graphs are isomorphic if there exists a one-to-one correspondence between their vertices and edges, preserving the adjacency relationships.
Example
Consider two graphs, G1 and G2, represented by the following adjacency matrices:
G1:
| v1 | v2 | v3 | |
|---|---|---|---|
| v1 | 0 | 1 | 0 |
| v2 | 1 | 0 | 1 |
| v3 | 0 | 1 | 0 |
G2:
| u1 | u2 | u3 | |
|---|---|---|---|
| u1 | 0 | 1 | 0 |
| u2 | 1 | 0 | 1 |
| u3 | 0 | 1 | 0 |
By comparing the adjacency matrices, we can see that they are identical. Therefore, G1 and G2 have the same vertex set and edge structure, indicating that they are isomorphic graphs.
Implications of Shared Vertices
When two graphs share the same vertex, it implies that they have a common structural element. This shared vertex may represent a shared property or relationship between the two graphs.
Shared Properties:
- Order:Graphs with the same vertex set have the same order.
- Degree:The degree of a vertex, which represents the number of edges incident to it, is the same in both graphs.
- Connectivity:If a vertex is a cut vertex in one graph, it will also be a cut vertex in the other graph.
Applications
Graphs with shared vertices find applications in various fields:
- Social networks:Shared vertices represent individuals with common connections.
- Transportation networks:Shared vertices represent intersections or junctions.
- Electrical circuits:Shared vertices represent nodes in a circuit.
Visual Representation
| Graph Pair | Equation | Vertex Set |
|---|---|---|
| G1 and G2 | Adjacency matrices | v1, v2, v3 |
| G3 and G4 | Incidence matrices | u1, u2, u3 |
| G5 and G6 | Edge lists | w1, w2, w3 |
Relationship between Graphs with Same Vertex:
The following diagram illustrates the relationship between graphs with the same vertex:

In this diagram, G1 and G2 are two graphs with the same vertex set v1, v2, v3. The vertices are represented by circles, and the edges are represented by lines connecting the circles. As you can see, G1 and G2 have the same structural arrangement of vertices and edges, indicating that they are isomorphic graphs.
FAQ Section
What is the significance of vertices in graph theory?
Vertices, also known as nodes, are fundamental building blocks of graphs. They represent the endpoints of edges and serve as the foundation for understanding the structure and properties of graphs.
How can we identify pairs of equations that generate graphs with the same vertex?
To identify pairs of equations that generate graphs with the same vertex, we can compare their coefficients and constants. Graphs with the same vertex will have equations with identical coefficients and constants.
What are the implications of two graphs having the same vertex?
When two graphs share the same vertex, it indicates that they have a common point of intersection. This shared vertex can provide valuable insights into the relationship between the two graphs and their underlying mathematical properties.