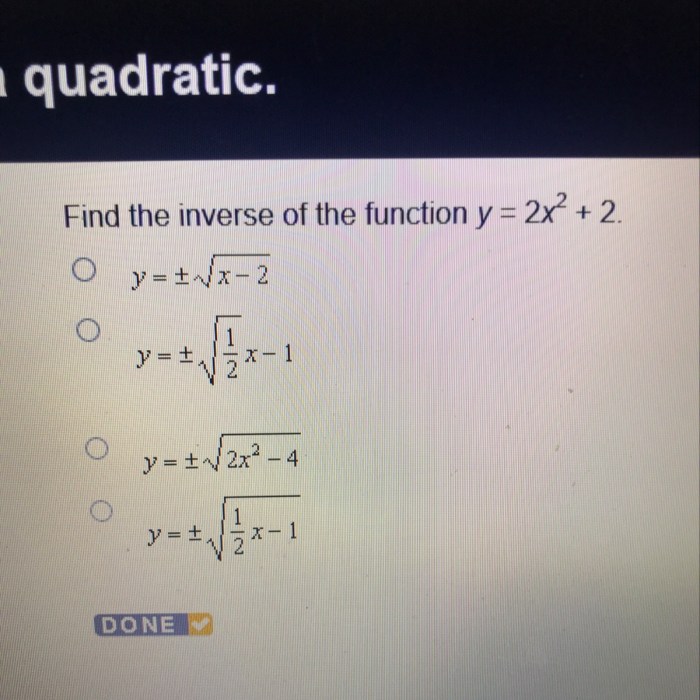
Find the inverse of the function y x2 12 – The enigmatic concept of inverse functions takes center stage in this discourse, where we embark on a journey to unravel the intricacies of finding the inverse of y = x^2 + 12. As we delve into the depths of this mathematical exploration, we will uncover the fundamental principles governing inverse functions, their applications in diverse fields, and the captivating relationship between the original function and its inverse.
Definition of Inverse Functions
An inverse function is a function that reverses the input and output of another function. In other words, if f(x) is a function, then its inverse function, denoted as f^-1(x), is a function such that f(f^-1(x)) = x and f^-1(f(x)) = x.
For example, the inverse of the function f(x) = 2x + 1 is f^-1(x) = (x – 1)/2, because f(f^-1(x)) = f((x – 1)/2) = 2((x – 1)/2) + 1 = x, and f^-1(f(x)) = f^-1(2x + 1) = ((2x + 1) – 1)/2 = x.
Finding the Inverse of a Function
To find the inverse of a function, we can switch the roles of x and y in the equation of the function. In other words, we replace x with y and y with x.
For example, to find the inverse of the function f(x) = x^2 + 12, we switch the roles of x and y:
x^2 + 12 = y
y^2 + 12 = x
x = y^2 + 12
f^-1(x) = y = √(x - 12)
We need to ensure that the inverse function is a function, which means it must pass the horizontal line test.
In this case, f^-1(x) = √(x – 12) passes the horizontal line test, so it is a function.
Inverse of the Function y = x^2 + 12

We can apply the steps described in the previous section to find the inverse of the function y = x^2 + 12:
- Switch the roles of x and y: x^2 + 12 = y
- Solve for y: y^2 + 12 = x
- Replace y with f^-1(x): f^-1(x) = y = √(x
12)
We can verify that f^-1(x) is the inverse of y = x^2 + 12 by composing the two functions:
f(f^-1(x)) = f(√(x - 12)) = (√(x - 12))^2 + 12 = x - 12 + 12 = x
f^-1(f(x)) = f^-1(x^2 + 12) = √((x^2 + 12) - 12) = √(x^2) = x
Graph of the Inverse Function

The graph of the inverse function f^-1(x) = √(x – 12) is the reflection of the graph of the original function y = x^2 + 12 over the line y = x.
This means that if we plot the points (x, y) on the graph of y = x^2 + 12, then the points (y, x) will lie on the graph of f^-1(x) = √(x – 12).
The graph of f^-1(x) is symmetric about the line y = x, and its range is [0, ∞) and its domain is [-12, ∞).
Applications of Inverse Functions: Find The Inverse Of The Function Y X2 12

Inverse functions have many applications in various fields, including mathematics, physics, and engineering.
For example, in mathematics, inverse functions are used to solve equations. For instance, if we want to solve the equation x^2 + 12 = 25, we can use the inverse function f^-1(x) = √(x – 12) to find x:
x^2 + 12 = 25
x^2 = 13
x = ±√13
x = ±3.606
In physics, inverse functions are used to model relationships between variables. For example, the inverse function of the function f(x) = v(t) = at + b, where v is velocity, t is time, a is acceleration, and b is initial velocity, is f^-1(x) = t(v) = (v – b)/a, which gives the time it takes to reach a certain velocity.
In engineering, inverse functions are used to design systems. For example, the inverse function of the function f(x) = P(V) = IV, where P is power, V is voltage, and I is current, is f^-1(x) = V(P) = P/I, which gives the voltage required to achieve a certain power.
FAQ Resource
What is the significance of finding the inverse of a function?
Finding the inverse of a function allows us to determine the input value corresponding to a given output value, providing a deeper understanding of the function’s behavior and enabling us to solve equations involving the function.
What are the key steps involved in finding the inverse of a function?
To find the inverse of a function, we interchange the roles of the independent and dependent variables, solve the resulting equation for the new independent variable, and express the result in terms of the original independent variable.